suivant: Exercice 19 - Représentation
monter: L'heure du code
précédent: Exercice 17 - Tri
Table des matières
Nous allons étudier la transformée discrète de Fourier et la façon
dont on peut la calculer efficacement. Etant donné un vecteur
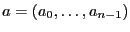 , la transformée discrète de Fourier de
, la transformée discrète de Fourier de 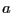 est un vecteur
est un vecteur
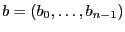 , noté
, noté 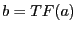 dont le
dont le
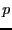 -ème élément est
-ème élément est
- Commençons par étudier les racines complexes de
 . Vous vous
doutez probablement
. Vous vous
doutez probablement  a deux racines carrées
a deux racines carrées 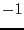 et
et
 . Vérifiez que
. Vérifiez que  ,
,
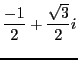 et
et
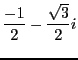 sont
sont 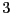 racines cubiques de
racines cubiques de  .
.
- Vérifiez que
 ,
, 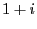 ,
, 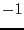 et
et 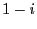 sont
sont 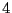 racines
quatrièmes de
racines
quatrièmes de  .
.
- Vérifiez que
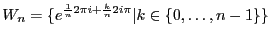 est l'ensemble
des racines
est l'ensemble
des racines  -èmes de
-èmes de  .
.
- Posons
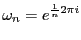 , véfifiez
que
, véfifiez
que
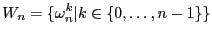 .
.
- Prouvez que pour tous
 et
et  ,
,
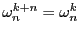 .
.
On considère l'algorithme
![\begin{algorithm}[H]
\dontprintsemicolon
\Fonction{$A(a, x, n)$}
{
$r \longl...
... $r \longleftarrow r + a_i \times y$\;
}
\Retourner{$r$}\;
}
\end{algorithm}](img385.gif)
- Soit
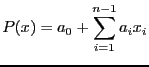 un
polynome de degré
un
polynome de degré 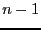 . Que vaut l'algorithme
. Que vaut l'algorithme 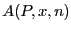 ?
?
- Quelle est la complexité de
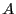 ?
?
- La méthode de Horner est basée sur la relation suivante
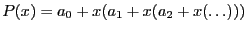 . Ecrivez
l'algorithme récursif
. Ecrivez
l'algorithme récursif 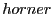 qui calcule
qui calcule 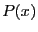 en utilisant cette
relation.
en utilisant cette
relation.
- Quelle est la complexité de
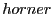 ?
?
- Soit
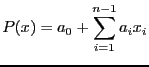 un
polynôme de degré
un
polynôme de degré 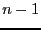 et
et 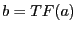 . Montrez que
. Montrez que
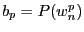 .
.
- Comment calculer
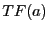 en utilisant le sous-programme
en utilisant le sous-programme 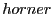 ?
Ecrivez le sous-programme
?
Ecrivez le sous-programme 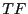 .
.
- On note
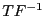 la transformée inverse de Fourier, nous admettrons
que si
la transformée inverse de Fourier, nous admettrons
que si
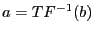 , alors
, alors
Ecrivez le sous-programme 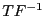 .
.
- Quelle sont les complexités de
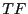 et de
et de 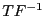 ?
?
- Prouvez que pour tous
 et
et  ,
,
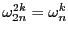 .
.
- Supposons que
 est pair, donc qu'il existe
est pair, donc qu'il existe 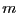 tel que
tel que 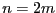 . Soit
. Soit
![$a^{[0]} = (a_0, a_2, \ldots, a_{2m})$](img398.gif) ,
,
![$a^{[1]} = (a_1,
a_3, \ldots, a_{2m+1})$](img399.gif) ,
,
![$b^{[0]} = TF(a^{[0]})$](img400.gif) et
et
![$b^{[1]} =
TF(a^{[1]})$](img401.gif) . Soit
. Soit
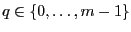 , montrez que
, montrez que
puis que
- Ecrire le sous-programme
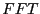 qui calcule la transformée discrète
de Fourier d'un vecteur de taille
qui calcule la transformée discrète
de Fourier d'un vecteur de taille 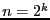 en utilisant la relation
de récurrence ci-dessus.
en utilisant la relation
de récurrence ci-dessus.
- Quelle est la complexité de
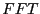 ?
?
- Supposons que
 est pair, donc qu'il existe
est pair, donc qu'il existe 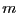 tel que
tel que 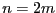 . Soit
. Soit
![$b^{[0]} = (b_0, b_2, \ldots, b_{2m})$](img407.gif) ,
,
![$b^{[1]} = (b_1,
b_3, \ldots, b_{2m+1})$](img408.gif) ,
,
![$y^{[0]} = TF^{-1}(b^{[0]})$](img409.gif) et
et
![$y^{[1]} =
TF^{-1}(b^{[1]})$](img410.gif) . Soit
. Soit
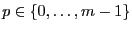 et
et
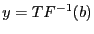 . Montrez que
. Montrez que
puis que
- Ecrire le sous-programme
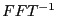 qui calcule la transformée
inverse de Fourier d'un vecteur de taille
qui calcule la transformée
inverse de Fourier d'un vecteur de taille 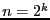 en utilisant la
relation de récurrence ci-dessus.
en utilisant la
relation de récurrence ci-dessus.
- Quelle est la complexité de
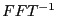 ?
?
- Ecrivez les fonctions du fichier fourier.c correspondant au
fichier fourier.h ci-dessous.
#ifndef FOURIER_H
#define FOURIER_H
#include"linkedList.h"
#include"complexe.h"
/*
Retourne la transformee discrete de Fourier du vecteur l.
Algorithme iteratif en O(n^2).
*/
linkedList* transformeeFourierIt(linkedList* l);
/*
Retourne la transformee discrete de Fourier inverse
du vecteur l. Algorithme iteratif en O(n^2).
*/
linkedList* transformeeInverseFourierIt(linkedList* l);
/*
Retourne la transformee discrete de Fourier du vecteur l, de taille
n = 2^m. Algorithme recursif en O(n log n).
*/
linkedList* FFT(linkedList* l);
/*
Retourne la transformee discrete de Fourier inverse
du vecteur l de taille n = 2^m. Algorithme recursif en
O(n log n).
*/
linkedList* inverseFFT(linkedList* l);
#endif
fourier.h
Vous utiliserez les fonctions auxiliaires suivantes :
- linkedList* uniteRacinesComplexe(complexe c, unsigned long
n), retourne les n racines n-ème de
 .
.
- complexe horner(link* p, complexe x), retourne
l'image de x par le polynôme p.




suivant: Exercice 19 - Représentation
monter: L'heure du code
précédent: Exercice 17 - Tri
Table des matières
klaus
2010-08-05
![]() , la transformée discrète de Fourier de
, la transformée discrète de Fourier de ![]() est un vecteur
est un vecteur
![]() , noté
, noté ![]() dont le
dont le
![]() -ème élément est
-ème élément est
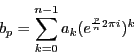
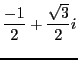 et
et
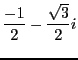 sont
sont ![\begin{algorithm}[H]
\dontprintsemicolon
\Fonction{$A(a, x, n)$}
{
$r \longl...
... $r \longleftarrow r + a_i \times y$\;
}
\Retourner{$r$}\;
}
\end{algorithm}](img385.gif)
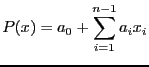 un
polynome de degré
un
polynome de degré 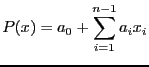 un
polynôme de degré
un
polynôme de degré