



suivant: Exercice 12 - Pgcd
monter: Problèmes
précédent: Exercice 10 - Tours
Table des matières
- Ecrire une fonction récursive unsigned long fibo(unsigned
long l) calculant le
 -ème nombre de fibonacci
-ème nombre de fibonacci 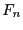 défini par
récurrence de la sorte :
défini par
récurrence de la sorte :
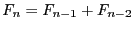 avec
avec 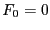 et
et
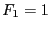 .
.
- Soit
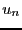 le nombre d'appels récursifs nécessaires pour calculer
le nombre d'appels récursifs nécessaires pour calculer
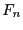 . Prouvez par récurrence que
. Prouvez par récurrence que 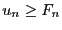 .
.
- Exprimer
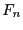 en fonction de
en fonction de  en résolvant la récurrence linéaire.
en résolvant la récurrence linéaire.
- Déterminer la complexité de fibo en passant par une borne
asymptotique inférieure.
- On considère la fonction
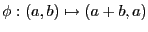 . Prouvez
que
. Prouvez
que
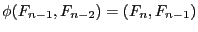 .
.
- On note
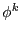 la composition de
la composition de  fonctions
fonctions 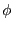 . Par
exemple,
. Par
exemple,
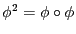 et
et
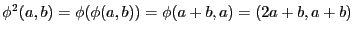 . Par convention,
. Par convention, 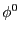 est la fonction identité, notée
est la fonction identité, notée 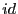 . Prouver par récurrence que
. Prouver par récurrence que
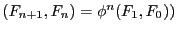 .
.
- Implémentez
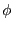 avec le sous-programme void phi(unsigned
long* l1, unsigned long* l2), notez que les deux variables
l1 et l2 sont passées en paramètre par référence.
avec le sous-programme void phi(unsigned
long* l1, unsigned long* l2), notez que les deux variables
l1 et l2 sont passées en paramètre par référence.
- Ecrivez le corps du sous-programme void applyF(void
(*f)(unsigned long*, unsigned long*), int n, unsigned long* l1,
unsigned long* l2), applyF applique n fois la
fonction f, en utilisant comme paramètre lors du premier
appel les variables pointées par l1 et l2.
- Utilisez applyF et phi pour coder unsigned
long fastFibo(unsigned long l)
- Majorer la complexité de applyF lorsqu'on lui passe le
sous-programme phi en paramètre, prouver ce résultat par
récurrence.
- Quelle est la complexité de fastFibo ? Porte-t-elle bien
son nom ?




suivant: Exercice 12 - Pgcd
monter: Problèmes
précédent: Exercice 10 - Tours
Table des matières
klaus
2010-08-05