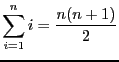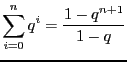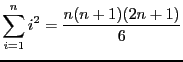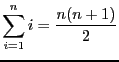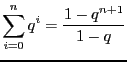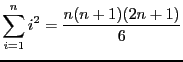suivant: Dérivée de fonctions puissance
monter: Exercices
précédent: Exercices
Table des matières
Prouver par récurrence les propriétés suivantes :
- Quel que soit
 ,
, 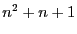 est impaire.
est impaire.
- Soit
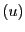 une suite définie par
une suite définie par 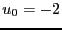 ,
,
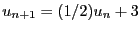 , alors
, alors

- Soit
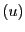 une suite définie par
une suite définie par 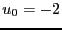 ,
,
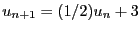 , alors
, alors

- Soit
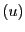 une suite définie par
une suite définie par 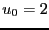 ,
,
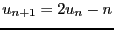 ,
alors
,
alors
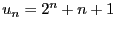
- Pour tout
 ,
,
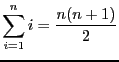
- Pour tout
 ,
,  ,
,
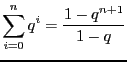
- Pour tout
 ,
,
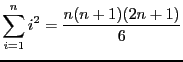




suivant: Dérivée de fonctions puissance
monter: Exercices
précédent: Exercices
Table des matières
klaus
2010-08-05