



suivant: Exemple
monter: Raisonnements par récurrence
précédent: Raisonnements par récurrence
Table des matières
Ce type de raisonnement ne s'applique que dans des propriétés faisant
intervenir des nombres entiers. Par exemple, ``Quel que soit  ,
,  est pair''. Pour prouver qu'une propriété est vérifiée
quelle que soit la valeur de
est pair''. Pour prouver qu'une propriété est vérifiée
quelle que soit la valeur de  , on effectue une preuve par
récurrence en procédant en deux
temps :
, on effectue une preuve par
récurrence en procédant en deux
temps :
- l'initialisation,
On prouve que pour
 (ou
(ou  , ça dépend des cas), la propriété
est vérifiée.
, ça dépend des cas), la propriété
est vérifiée.
- l'hérédité, on prouve que si la propriété est vérifiée au
rang
 , alors elle l'est au rang
, alors elle l'est au rang 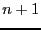 .
.




suivant: Exemple
monter: Raisonnements par récurrence
précédent: Raisonnements par récurrence
Table des matières
klaus
2010-08-05
![]() ,
, ![]() est pair''. Pour prouver qu'une propriété est vérifiée
quelle que soit la valeur de
est pair''. Pour prouver qu'une propriété est vérifiée
quelle que soit la valeur de ![]() , on effectue une preuve par
récurrence en procédant en deux
temps :
, on effectue une preuve par
récurrence en procédant en deux
temps :