



suivant: Exercice 6 - PARTITION/SUBSET
monter: Un espoir vain
précédent: Exercice 4 - ENSEMBLE
Table des matières
Le problème SUBSET SUM, est défini comme suit
:
On peut montrer par une réduction de 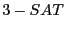 que
que  est
NP-Complet. Effectuons la transformation suivante :
est
NP-Complet. Effectuons la transformation suivante :
- A chaque variable
 , on associe deux valeurs
, on associe deux valeurs  et
et 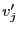 dont la représentation décimale comporte
dont la représentation décimale comporte  chiffres.
chiffres.
- Les
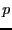 premiers chiffres représentent les clauses. Le
premiers chiffres représentent les clauses. Le 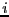 -ème
chiffre (
-ème
chiffre (
 ) de
) de  prend la valeur
prend la valeur  si
si  apparaît dans
apparaît dans 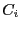 ,
, 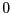 sinon. Le
sinon. Le 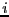 -ème
chiffre (
-ème
chiffre (
 ) de
) de 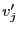 prend la valeur
prend la valeur  si
si  apparaît dans
apparaît dans 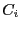 ,
, 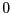 sinon.
sinon.
- Les
 derniers chiffres représentent l'indice de la variable
derniers chiffres représentent l'indice de la variable
 , le
, le  -ème chiffre de
-ème chiffre de  et de
et de 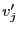 prend la
valeur
prend la
valeur  , les
, les 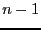 autres chiffres prennent la valeur
autres chiffres prennent la valeur 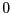 .
.
- A chaque clause
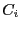 , on associe
, on associe 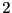 valeurs
valeurs  et
et
 de
de  chiffres dont le
chiffres dont le 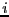 -ème chiffre vaut
-ème chiffre vaut  et
tous les autres
et
tous les autres 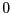 .
.
- On prend comme nombre
 la valeur dont les
la valeur dont les 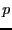 premiers chiffres
valent
premiers chiffres
valent 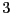 et les
et les  derniers
derniers  .
.
Utilisez la réduction polynomiale ci-dessus pour montrer que SUBSET
SUM est NP-Complet.




suivant: Exercice 6 - PARTITION/SUBSET
monter: Un espoir vain
précédent: Exercice 4 - ENSEMBLE
Table des matières
klaus
2010-08-05
![]() que
que ![]() est
NP-Complet. Effectuons la transformation suivante :
est
NP-Complet. Effectuons la transformation suivante :