



suivant: Application
monter: Réductions polynomiales
précédent: Définition
Table des matières
Montrons que le problème  (cycle hamiltonien) est
moins difficile que
(cycle hamiltonien) est
moins difficile que  (voyageur de commerce). Pour cela,
construisons une fonction
(voyageur de commerce). Pour cela,
construisons une fonction 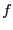 prenant en paramètre une instance du
problème
prenant en paramètre une instance du
problème  , et créant une instance
, et créant une instance 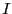 du problème
du problème  . Il est très
important de déterminer
. Il est très
important de déterminer 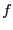 de sorte que
de sorte que 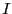 soit à réponse oui
si et seulement si
soit à réponse oui
si et seulement si  est à réponse oui. Rappelons la
définition de
est à réponse oui. Rappelons la
définition de  dans un graphe non orienté :
dans un graphe non orienté :
- Données : un graphe
 non orienté
non orienté
- Question : existe-t-il un cycle hamiltonien dans
 ?
?
Ainsi que la définition de  ,
,
- Données : un graphe
 non orienté muni d'une valuation
non orienté muni d'une valuation  ,
une constante
,
une constante 
- Question : existe-t-il dans un
 un cycle hamiltonien de
longueur inférieure ou égale à
un cycle hamiltonien de
longueur inférieure ou égale à  ?
?
Nous définissons 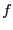 de la sorte,
de la sorte, 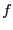 prend en paramètre les données
de
prend en paramètre les données
de  , à savoir le graphe
, à savoir le graphe  , on définit l'instance
, on définit l'instance  de la sorte
de la sorte
-
 ,
,  contient toutes les paires de
sommets qu'il est possible de former avec les sommets de
contient toutes les paires de
sommets qu'il est possible de former avec les sommets de
 . Autrement dit,
. Autrement dit,  est un graphe complet.
est un graphe complet.
 si
si  ,
,  si
si  . Autrement
dit, les arêtes de
. Autrement
dit, les arêtes de  ont la valeur
ont la valeur  si elle se
trouvaient dans
si elle se
trouvaient dans 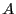 , et toutes les arêtes qui ont été ajoutées pour
obtenir un graphe complet ont la valeur
, et toutes les arêtes qui ont été ajoutées pour
obtenir un graphe complet ont la valeur 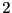 .
.
 .
.
Il est maintenant nécessaire de montrer que 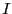 est une instance à
réponse oui si et seulement si
est une instance à
réponse oui si et seulement si  est une instance à réponse oui.
est une instance à réponse oui.
- Soit
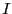 une instance de
une instance de  à réponse oui. Alors il existe un
cycle hamiltonien dans
à réponse oui. Alors il existe un
cycle hamiltonien dans  . La longueur de ce cycle dans
. La longueur de ce cycle dans  est
est  , à
savoir le nombre de sommets. La longueur de ce cycle est
aussi
, à
savoir le nombre de sommets. La longueur de ce cycle est
aussi  dans
dans  , car les arêtes empruntées dans
, car les arêtes empruntées dans
 étaient toutes de valuation
étaient toutes de valuation  .
.
- Soit
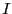 une instance de
une instance de  telle que
telle que  est à réponse
oui. Comme
est à réponse
oui. Comme  est à réponse oui, alors il existe un cycle
hamiltonien de longueur
est à réponse oui, alors il existe un cycle
hamiltonien de longueur  . Comme ce cycle passe par
. Comme ce cycle passe par  arêtes, et que toutes les arêtes de
arêtes, et que toutes les arêtes de  sont de valuation
sont de valuation  ou
ou 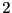 , alors ce cycle n'emprunte que des arêtes de valuation
, alors ce cycle n'emprunte que des arêtes de valuation
 . Comme les arêtes de valuation
. Comme les arêtes de valuation  de
de  sont aussi des
arêtes de
sont aussi des
arêtes de  , alors il existe un cycle hamiltonien dans
, alors il existe un cycle hamiltonien dans  .
.




suivant: Application
monter: Réductions polynomiales
précédent: Définition
Table des matières
klaus
2010-08-05
![]() (cycle hamiltonien) est
moins difficile que
(cycle hamiltonien) est
moins difficile que ![]() (voyageur de commerce). Pour cela,
construisons une fonction
(voyageur de commerce). Pour cela,
construisons une fonction ![]() prenant en paramètre une instance du
problème
prenant en paramètre une instance du
problème ![]() , et créant une instance
, et créant une instance ![]() du problème
du problème ![]() . Il est très
important de déterminer
. Il est très
important de déterminer ![]() de sorte que
de sorte que ![]() soit à réponse oui
si et seulement si
soit à réponse oui
si et seulement si ![]() est à réponse oui. Rappelons la
définition de
est à réponse oui. Rappelons la
définition de ![]() dans un graphe non orienté :
dans un graphe non orienté :
![]() ,
,
![]() de la sorte,
de la sorte, ![]() prend en paramètre les données
de
prend en paramètre les données
de ![]() , à savoir le graphe
, à savoir le graphe ![]() , on définit l'instance
, on définit l'instance ![]() de la sorte
de la sorte
![]() est une instance à
réponse oui si et seulement si
est une instance à
réponse oui si et seulement si ![]() est une instance à réponse oui.
est une instance à réponse oui.