



suivant: Théorie de la complexité
monter: Les fonctions
précédent: Exercice 5 - Prise
Table des matières
Un enseignant a donné  notes de contrôle continu à ses
notes de contrôle continu à ses  élèves, et une note de partiel pour chaque élève. On note
élèves, et une note de partiel pour chaque élève. On note 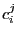 la
note obtenue par le
la
note obtenue par le 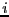 -ème élève au
-ème élève au 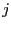 -ème contrôle continu, et
-ème contrôle continu, et
 la note de partiel du
la note de partiel du 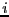 -ème élève. Il souhaite déterminer le
jeu de coefficients qui maximise la moyenne générale de la classe.
-ème élève. Il souhaite déterminer le
jeu de coefficients qui maximise la moyenne générale de la classe.
- Comment résoudre ce problème ? Utilisez GLPK pour résoudre
l'instance
![\begin{clisting}
double notesPartiel[N] = {10, 13, 2, 4.5, 9, 12, 16, 8, 5, 12}...
...13};
double notesCC2[N] = { 9, 18, 7, 8, 11, 3, 13, 10, 7, 19};
\end{clisting}](img748.gif)
- Que remarquez-vous ?
- Le responsable pédagogique est en total désaccord, il considère que
la note de partiel doit avoir un coefficient au moins égal à
 et que deux notes de contrôle continu doivent avoir des
coefficients au moins égaux à
et que deux notes de contrôle continu doivent avoir des
coefficients au moins égaux à 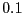 . Comment tenir compte de ces
contraintes ?
. Comment tenir compte de ces
contraintes ?
- En raison d'un petit nombre de notes très élevées à certains
examens, la moyenne générale de la classe est bonne malgré le fait
que beaucoup d'élèves ont une moyenne très basse. L'enseignant
décide donc de changer de critère et de maximiser la moyenne la
plus basse. Comment procéder ?
- Vérifiez la solution de la question précédente en calculant les
moyennes de tous les élèves avec les coefficients donnés par GLPK
(ne le calculez pas à la main, programmez-le...).




suivant: Théorie de la complexité
monter: Les fonctions
précédent: Exercice 5 - Prise
Table des matières
klaus
2010-08-05
![]() notes de contrôle continu à ses
notes de contrôle continu à ses ![]() élèves, et une note de partiel pour chaque élève. On note
élèves, et une note de partiel pour chaque élève. On note ![]() la
note obtenue par le
la
note obtenue par le ![]() -ème élève au
-ème élève au ![]() -ème contrôle continu, et
-ème contrôle continu, et
![]() la note de partiel du
la note de partiel du ![]() -ème élève. Il souhaite déterminer le
jeu de coefficients qui maximise la moyenne générale de la classe.
-ème élève. Il souhaite déterminer le
jeu de coefficients qui maximise la moyenne générale de la classe.
![\begin{clisting}
double notesPartiel[N] = {10, 13, 2, 4.5, 9, 12, 16, 8, 5, 12}...
...13};
double notesCC2[N] = { 9, 18, 7, 8, 11, 3, 13, 10, 7, 19};
\end{clisting}](img748.gif)