



suivant: Terminaison
monter: Invariants de boucle
précédent: Le principe
Table des matières
On divise deux entiers strictement positifs 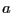 et
et 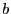 en déterminant
deux entiers
en déterminant
deux entiers 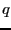 et
et 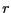 tels que
tels que  avec
avec  . Voici un algorithme déterminant
. Voici un algorithme déterminant 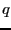 et
et 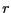 :
:
![\begin{algorithm}[H]
\dontprintsemicolon
$q \longleftarrow 0$\;
$r \longleftarro...
...$}
{
$q \longleftarrow q + 1$\;
$r \longleftarrow r - b$\;
}
\end{algorithm}](img59.gif)
On choisit comme invariant de boucle la propriété  .
.
- Comme
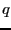 est initialisé à
est initialisé à 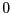 et
et 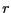 à
à 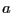 , alors la propriété
, alors la propriété
 est vérifiée avant le premier passage dans la
boucle.
est vérifiée avant le premier passage dans la
boucle.
- Avant une itération arbitraire, supposons que l'on ait
 ,
montrons que cette propriété est conservée par cette
itération. Soient
,
montrons que cette propriété est conservée par cette
itération. Soient 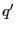 la valeur de
la valeur de 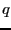 à la fin de
l'itération et
à la fin de
l'itération et 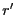 la valeur de
la valeur de 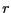 à la fin de
l'itération. Nous devons montrer que
à la fin de
l'itération. Nous devons montrer que
 . On
a
. On
a
 et
et
 , alors
, alors
 . La propriété est bien
conservée.
. La propriété est bien
conservée.
klaus
2010-08-05
![]() et
et ![]() en déterminant
deux entiers
en déterminant
deux entiers ![]() et
et ![]() tels que
tels que ![]() avec
avec ![]() . Voici un algorithme déterminant
. Voici un algorithme déterminant ![]() et
et ![]() :
:
![\begin{algorithm}[H]
\dontprintsemicolon
$q \longleftarrow 0$\;
$r \longleftarro...
...$}
{
$q \longleftarrow q + 1$\;
$r \longleftarrow r - b$\;
}
\end{algorithm}](img59.gif)
![]() .
.