



suivant: Exercice 6 - Ordonnancement
monter: Exercices
précédent: Exercice 4 - le
Table des matières
Soit  un graphe,
un graphe,  une constante strictement
positive. On
s'intéresse à la
une constante strictement
positive. On
s'intéresse à la  -colorabilité du graphe
-colorabilité du graphe  (i.e. peut-on colorier
le graphe
(i.e. peut-on colorier
le graphe  avec
avec  couleurs ?). Nous allons créer un graphe
couleurs ?). Nous allons créer un graphe
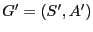 à partir de
à partir de  en procédant de la façon suivante :
en procédant de la façon suivante :
- A chaque sommet
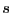 de
de  , on associe
, on associe  sommets de
sommets de  , notés
, notés
 , tous
reliés entre eux par des arêtes.
, tous
reliés entre eux par des arêtes.
- Pour chaque arête
 de
de  , et chaque couleur
, et chaque couleur 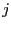 , on relie
dans
, on relie
dans  les sommets
les sommets  et
et 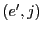 . Notez bien que
comme les sommets sont des couples, les arêtes sont des
paires de couples.
. Notez bien que
comme les sommets sont des couples, les arêtes sont des
paires de couples.
Plus formellement,
-
est un ensemble de couples (sommet de  /couleur).
/couleur).
-
avec
un ensemble d'arêtes formant  sous-graphes complets de
sous-graphes complets de
 sommets et
sommets et
un ensemble d'arêtes interconnectant ces sous-graphes.
Le but de cet exercice est de montrer qu'en trouvant un ensemble
stable de  sommets
dans
sommets
dans  , on trouve aussi une
, on trouve aussi une  -coloration de
-coloration de  .
.
- Soit
 le graphe de l'exercice précédent, on pose
le graphe de l'exercice précédent, on pose  . Représentez graphiquement
. Représentez graphiquement  .
.
- Donnez une définition en français (avec des mots) de ce qu'est un
ensemble stable.
- Ce problème (existe-t-il un ensemble stable de
 sommets dans
sommets dans
 ?) est-il NP-Complet ?
?) est-il NP-Complet ?
- Donnez un ensemble stable de
 sommets dans ce graphe.
sommets dans ce graphe.
- Utilisez cet ensemble stable pour déterminer une
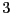 -coloration de
-coloration de  .
.
- Démontrez de façon formelle et avec le plus de rigueur possible que,
étant donné un graphe
 arbitraire, un nombre
arbitraire, un nombre 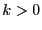 ,
,  est
est
 -colorable si et seulement s'il existe un ensemble stable de
-colorable si et seulement s'il existe un ensemble stable de
 sommets dans
sommets dans  .
.




suivant: Exercice 6 - Ordonnancement
monter: Exercices
précédent: Exercice 4 - le
Table des matières
klaus
2010-08-05
![]() un graphe,
un graphe, ![]() une constante strictement
positive. On
s'intéresse à la
une constante strictement
positive. On
s'intéresse à la ![]() -colorabilité du graphe
-colorabilité du graphe ![]() (i.e. peut-on colorier
le graphe
(i.e. peut-on colorier
le graphe ![]() avec
avec ![]() couleurs ?). Nous allons créer un graphe
couleurs ?). Nous allons créer un graphe
![]() à partir de
à partir de ![]() en procédant de la façon suivante :
en procédant de la façon suivante :
![]() sommets
dans
sommets
dans ![]() , on trouve aussi une
, on trouve aussi une ![]() -coloration de
-coloration de ![]() .
.