



suivant: Sac à dos
monter: Problèmethèque
précédent: Coloration
Table des matières
Soit  un graphe orienté (ou non) muni d'une valuation de arêtes
un graphe orienté (ou non) muni d'une valuation de arêtes
 .
Un chemin
.
Un chemin 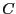 de longueur
de longueur 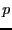 dans
dans  est un
est un 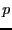 -uplet
-uplet
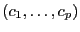 d'éléments de
d'éléments de 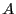 tel que si
tel que si
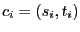 , alors pour tout
, alors pour tout
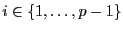 ,
, 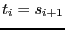 .
. 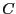 est un chemin de
est un chemin de 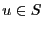 à
à 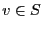 si
si 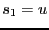 et
et 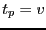 .
.
Le problème du plus court chemin dans un graphe valué se définit comme
suit :
- données : un graphe
 valué, deux sommets
valué, deux sommets  et
et 
- question : trouver le plus court chemin de
 à
à  dans
dans  .
.
Ce problème est polynomial, Les deux algorithmes les plus connus sont
- Dijkstra : très rapide,
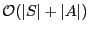 dans le
pire des cas, mais
ne fonctionne qu'avec les valuations positives, ne nécessite pas le
parcours de tout le graphe.
dans le
pire des cas, mais
ne fonctionne qu'avec les valuations positives, ne nécessite pas le
parcours de tout le graphe.
- Bellman : un peu moins rapide, il présente l'avantage de
fonctionner avec des valuations négatives, sauf si le graphe
contient un circuit absorbant (i.e. négatif).




suivant: Sac à dos
monter: Problèmethèque
précédent: Coloration
Table des matières
klaus
2010-08-05
![]() un graphe orienté (ou non) muni d'une valuation de arêtes
un graphe orienté (ou non) muni d'une valuation de arêtes
![]() .
Un chemin
.
Un chemin ![]() de longueur
de longueur ![]() dans
dans ![]() est un
est un ![]() -uplet
-uplet
![]() d'éléments de
d'éléments de ![]() tel que si
tel que si
![]() , alors pour tout
, alors pour tout
![]() ,
, ![]() .
. ![]() est un chemin de
est un chemin de ![]() à
à ![]() si
si ![]() et
et ![]() .
.