



suivant: Algorithmes itératifs
monter: Algorithmes de complexité polynomiale
précédent: Exercice 3 - Tri
Table des matières
Un arbre binaire est un arbre dont chaque noeud a 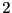 fils. Un arbre vide, donc sans noeud, noté
fils. Un arbre vide, donc sans noeud, noté  , est de
profondeur
, est de
profondeur
 . Un noeud est une feuille si ses deux
fils sont des arbres vides. Soit
. Un noeud est une feuille si ses deux
fils sont des arbres vides. Soit 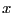 un noeud,
un noeud, 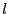 et
et 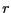 ses fils la
hauteur de
ses fils la
hauteur de 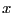 est alors
est alors
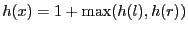 . La hauteur
d'un arbre binaire est la hauteur de son noeud de hauteur maximale,
donc de la racine. La racine
. La hauteur
d'un arbre binaire est la hauteur de son noeud de hauteur maximale,
donc de la racine. La racine 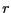 est de profondeur
est de profondeur  , tout
noeud
, tout
noeud 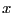 de père
de père  est de profondeur
est de profondeur
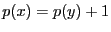 .
.
- Quelle est la hauteur d'une feuille d'un arbre binaire?
- Comment disposer les noeuds pour que la hauteur d'un arbre binaire à
 noeuds soit minimale ?
noeuds soit minimale ?
- Nous ne considérerons dorénavant que des arbres binaires dans
lesquels les noeuds sont disposés comme décrit dans la question
précédente. Soit
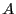 un arbre de profondeur
un arbre de profondeur  , déterminer pour
tout
, déterminer pour
tout
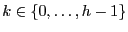 le nombre de noeuds de
le nombre de noeuds de 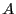 dont la
profondeur est
dont la
profondeur est  .
.
- Encadrer le nombre de noeuds de profondeur
 .
.
- Donner la borne inférieure du nombre
 de noeuds d'un arbre
binaire de profondeur
de noeuds d'un arbre
binaire de profondeur  .
.
- Majorer
 en fonction de
en fonction de  .
.
- Donner une borne asymptotique supérieure de la hauteur
 d'un arbre binaire à
d'un arbre binaire à  noeuds de hauteur minimale.
noeuds de hauteur minimale.




suivant: Algorithmes itératifs
monter: Algorithmes de complexité polynomiale
précédent: Exercice 3 - Tri
Table des matières
klaus
2010-08-05
![]() fils. Un arbre vide, donc sans noeud, noté
fils. Un arbre vide, donc sans noeud, noté ![]() , est de
profondeur
, est de
profondeur
![]() . Un noeud est une feuille si ses deux
fils sont des arbres vides. Soit
. Un noeud est une feuille si ses deux
fils sont des arbres vides. Soit ![]() un noeud,
un noeud, ![]() et
et ![]() ses fils la
hauteur de
ses fils la
hauteur de ![]() est alors
est alors
![]() . La hauteur
d'un arbre binaire est la hauteur de son noeud de hauteur maximale,
donc de la racine. La racine
. La hauteur
d'un arbre binaire est la hauteur de son noeud de hauteur maximale,
donc de la racine. La racine ![]() est de profondeur
est de profondeur ![]() , tout
noeud
, tout
noeud ![]() de père
de père ![]() est de profondeur
est de profondeur
![]() .
.