



suivant: Exercice 13 - Pavage
monter: Problèmes
précédent: Exercice 11 - Suite
Table des matières
Le plus grand commun diviseur de deux entiers relatifs 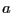 et
et 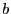 ,
noté
,
noté 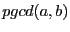 , est défini par la relation de récurrence
, est défini par la relation de récurrence
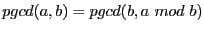 , avec
, avec
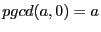 .
.
- Ecrire une fonction récursive calculant le
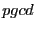 de deux entiers
relatifs.
de deux entiers
relatifs.
- Ecrire une fonction itérative retournant le
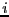 -ème nombre de
fibonacci.
-ème nombre de
fibonacci.
- Ecrire les deux sous-programmes unsigned long pgcd(unsigned
long a, unsigned long b) et unsigned long
fibonacci(unsigned long l)
- Tester la fonction
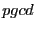 avec des nombres de fibonacci
consécutifs. Qu'observez-vous ?
avec des nombres de fibonacci
consécutifs. Qu'observez-vous ?
- Si on s'intéresse au nombre d'appels récursifs nécessaires pour
calculer un
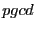 , quel est le pire des cas ?
, quel est le pire des cas ?
- Quel est la valeur du quotient
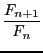 ?
?
- En déduire que les entrées de la forme
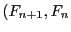 forment les pires
cas.
forment les pires
cas.
- Combien d'itérations sont nécesaires pour calculer
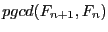 ?
?
- Prouver que
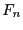 est majoré par une suite géométrique.
est majoré par une suite géométrique.
- Prouver que le nombre d'appels récursifs est majoré par un
logarithme de base
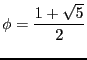 .
.
- Quelle est la complexité de
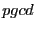 , est-ce efficace ?
, est-ce efficace ?




suivant: Exercice 13 - Pavage
monter: Problèmes
précédent: Exercice 11 - Suite
Table des matières
klaus
2010-08-05
![]() et
et ![]() ,
noté
,
noté ![]() , est défini par la relation de récurrence
, est défini par la relation de récurrence
![]() , avec
, avec
![]() .
.
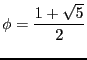 .
.