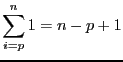
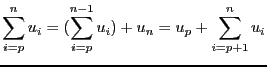
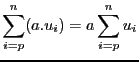
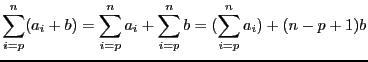
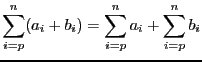
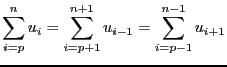
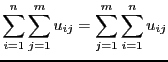
Parmi les outils mathématiques permettant d'évaluer la complexité d'un algorithme se trouvent les sommations. Commençons par rappeler quelques propriétés :
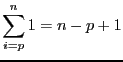
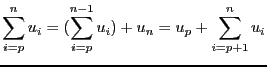
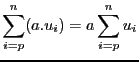
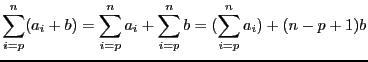
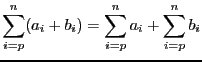
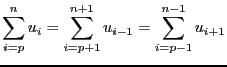
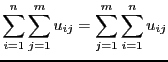
Bien que le ![]() soit prioritaire sur le
soit prioritaire sur le ![]() mais pas sur le
mais pas sur le
![]() , il usuel pour éviter toute confusion de rajouter des
parenthèses, même inutiles. Parmi les sommes que vous devez maîtriser
parfaitement figurent les deux suivantes :
, il usuel pour éviter toute confusion de rajouter des
parenthèses, même inutiles. Parmi les sommes que vous devez maîtriser
parfaitement figurent les deux suivantes :
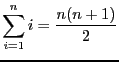 (série
arithmétique)
(série
arithmétique)
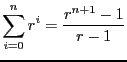 (série géométrique)
(série géométrique)
On se ramène souvent à ce type de formule en algorithmique.