Factorielle

Étudions un exemple,

Tout d'abord, on remarque que $factorielleT$ est bien une fonction récursive terminale. Ensuite observons que si l'on invoque $factorielleT(n, 1)$, on obtient la séquence suivante :

$$(n, 1) \longrightarrow (n - 1, n)\longrightarrow (n - 2, n \times (n-1)) \longrightarrow \ldots$$

$$\ldots \longrightarrow (i, \prod_{k=i+1}^n k) \longrightarrow \ldots$$

$$\ldots \longrightarrow (2, \prod_{k=3}^n k) \longrightarrow (1, \prod_{k=2}^n k) \longrightarrow (0, \prod_{k=1}^n k)$$

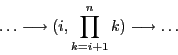
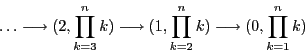
Au moment où la condition d'arrêt est vérifiée, le paramètre $r$ contient la valeur $\prod_{k=1}^n k$, à savoir $n!$. On se sert de l'accumulateur pour fabriquer le résultat. Démontrons par récurrence sur $n$ que $factorielleT(n, r) = r(n!)$ :

• Tout d'abord, on constate que $factorielleT(0, r) = r$
• Supposons que $factorielleT(n - 1, r^\prime)$ retourne la valeur $(n - 1)! \times r^\prime$, donc $factorielleT(n - 1, n \times r) = (n - 1)!(r \times n) = r(n!)$. D'où $factorielleT(n, r) = factorielleT(n - 1, n \times r) = r(n!)$

On en déduit qu'en posant $r = 1$, on a $factorielleT(n, 1) = n!$ On encapsule $factorielleT$ dans le sous-programme $factorielle$ que l'on redéfinit de la sorte :