



suivant: Applications directes du cours
monter: RSA
précédent: Déchiffrement
Table des matières
D'après le théorème d'Euler, pour tout
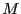 premier avec
premier avec 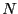 ,
,
Plus généralement, pour tout  entier relatif,
entier relatif,
Ce qui s'écrit aussi
et de ce fait
Comme
il convient de déterminer 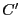 tel que
tel que
ce qui s'écrit plus simplement comme une relation de Bezout
Notez que la connaissance de 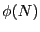 est indispensable si on
souhaite trouver
est indispensable si on
souhaite trouver 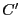 . Etant donné
. Etant donné 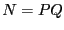 le produit de
nombres premiers
le produit de
nombres premiers 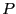 et
et 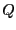 , on a
, on a
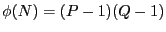 . Donc pour
connaître
. Donc pour
connaître 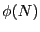 , il est nécessaire de connaître la décomposition
de
, il est nécessaire de connaître la décomposition
de 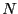 en produit de facteurs premiers. Donc, retrouver
en produit de facteurs premiers. Donc, retrouver 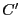 à
partir de
à
partir de 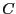 oblige le cryptanalyste à passer par une factorisation
de
oblige le cryptanalyste à passer par une factorisation
de 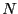 , problème connu pour être difficile.
, problème connu pour être difficile.




suivant: Applications directes du cours
monter: RSA
précédent: Déchiffrement
Table des matières
klaus
2010-08-05
![]() premier avec
premier avec ![]() ,
,