Le théorème suivant est une généralisation du petit théorème de Fermat
s'appliquant dans les cas où l'on connaît ![]() .
.
Par exemple, si ![]() , et
, et ![]() , alors
, alors
![]() , on a bien
, on a bien
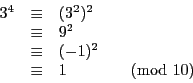
Si ![]() et
et ![]() , alors
, alors
![]() , et on a
bien
, et on a
bien
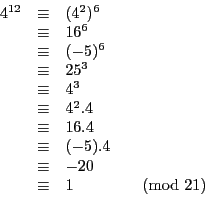
Par exemple, si ![]() et
et ![]() , l'inverse de
, l'inverse de ![]() dans
dans ![]() est
est
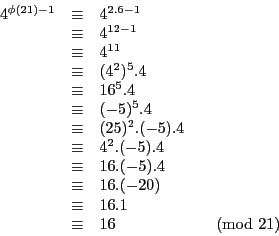
On le vérifie aisément en calculant
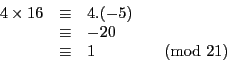
L'inverse modulo ![]() (
(![]() et
et ![]() premiers et distincts) de
premiers et distincts) de ![]() (inversible dans
(inversible dans ![]() ) est donc
) est donc
![]() .
.