suivant: Exercice 8 - Tranche
monter: ComplexitÚ
précédent: Morceaux choisis
Table des matières
Nous représenterons un polynôme
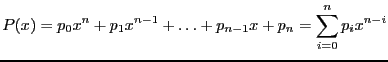 de
degré
de
degré  à l'aide d'un tableau
à l'aide d'un tableau
![$[p_0, p_1, \ldots, p_{n-1}, p_n]$](img150.gif) à
à
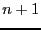 éléments. Notez bien que ce tableau est indicé à partir de
éléments. Notez bien que ce tableau est indicé à partir de 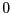 .
.
- Que fait la fonction suivante ?
![\begin{algorithm}[H]
\dontprintsemicolon
\Fonction{$mystery([p_0, \ldots, p_n]...
...me \longleftarrow somme + terme$\;
}
\Retourner{$somme$}\;
}
\end{algorithm}](img152.gif)
- Quelle est la complexité de
 ?
?
- Écrire la procédure
![$derive([p_0, \ldots, p_n])$](img154.gif) remplaçant
remplaçant 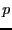 par
sa dérivée.
par
sa dérivée.
- Prouver que
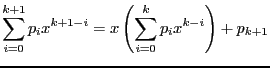
- Déduire de la relation ci-dessus une fonction
![$evalue([p_0, \ldots,
p_n], x)$](img156.gif) prenant
prenant 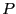 et
et 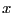 en paramètres, et retournant
en paramètres, et retournant 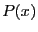 .
.
- Prouver la validité de la fonction d'évaluation, vous utiliserez les
questions précédentes.
- Quelle est la complexité de
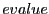 ?
?
klaus
2010-08-05
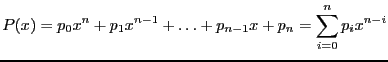 de
degré
de
degré 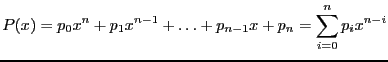 de
degré
de
degré ![]() à l'aide d'un tableau
à l'aide d'un tableau
![]() à
à
![]() éléments. Notez bien que ce tableau est indicé à partir de
éléments. Notez bien que ce tableau est indicé à partir de ![]() .
.
![\begin{algorithm}[H]
\dontprintsemicolon
\Fonction{$mystery([p_0, \ldots, p_n]...
...me \longleftarrow somme + terme$\;
}
\Retourner{$somme$}\;
}
\end{algorithm}](img152.gif)