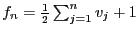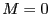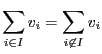suivant: Introduction à la cryptographie
monter: Un espoir vain
précédent: Exercice 7 - PARTITION/SAC
Table des matières
- Montrez que SCHEDULING
 NP.
NP.
- Etant donné le problème PARTITION :
- Données : Un ensemble de
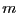 valeurs
valeurs
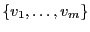 .
.
- Question : Existe-t-il un sous-ensemble
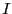 de
de
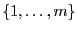 tel que
tel que
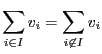
Autrement dit, est-il possible de partitionner l'ensemble
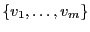 en deux sous-ensembles dont la somme des valeurs est égale ?
L'instance de PARTITION suivante,
en deux sous-ensembles dont la somme des valeurs est égale ?
L'instance de PARTITION suivante, 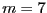 ,
,
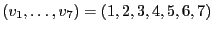 est-elle à réponse "oui" ?
Vous démontrerez la justesse de votre réponse.
est-elle à réponse "oui" ?
Vous démontrerez la justesse de votre réponse.
- Nous savons que PARTITION est NP-Complet. Nous allons
montrer à l'aide d'une réduction polynomiale
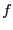 , que PARTITION
, que PARTITION
 SCHEDULING. Nous construisons une fonction
SCHEDULING. Nous construisons une fonction 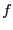 qui à toute
instance de PARTITION associe une instance de SCHEDULING
définie comme suit :
Déterminer l'image de l'instance
qui à toute
instance de PARTITION associe une instance de SCHEDULING
définie comme suit :
Déterminer l'image de l'instance
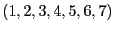 par la
fonction
par la
fonction 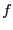 . Vous présenterez votre solution sous forme d'un
tableau, vous préciserez les valeurs de toutes les données du
problème.
. Vous présenterez votre solution sous forme d'un
tableau, vous préciserez les valeurs de toutes les données du
problème.
- L'image de cette instance est-elle à réponse "oui" ? Vous démontrerez la
justesse de votre réponse en donnant les valeurs de début
d'exécution si c'est le cas, ou bien une preuve d'impossibilité dans
le cas contraire.
- Montrez, sans excès de formalisme, que
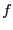 est polynomiale.
est polynomiale.
- Montrer que toute instance de PARTITION à réponse oui a une image
par
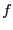 à réponse oui.
à réponse oui.
- Montrer que toute instance de PARTITION dont l'image est à réponse
oui est à réponse oui.
- SCHEDULING est-il NP-Complet ? Justifiez votre réponse.




suivant: Introduction à la cryptographie
monter: Un espoir vain
précédent: Exercice 7 - PARTITION/SAC
Table des matières
klaus
2010-08-05
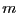 valeurs
valeurs
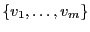 .
.
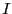 de
de
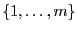 tel que
tel que
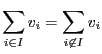
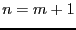
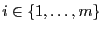 ,
, 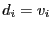 ,
, 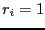 ,
,
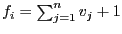
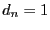 ,
,
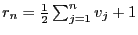 ,
,