



suivant: Couverture
monter: Problèmethèque
précédent: Voyageur de commerce
Table des matières
Soit une expression booléenne à  variables sous forme clausale
(conjonction de disjonctions), par exemple,
variables sous forme clausale
(conjonction de disjonctions), par exemple,
Les clauses (contenant des
disjonctions) sont notées
Toute clause est formée de 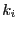 littéraux
littéraux
chaque littéral 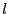 est soit une variable (
est soit une variable (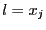 ),
soit la négation d'une variable (
),
soit la négation d'une variable (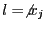 ). Une affectation
). Une affectation
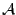 des variables est une application de
des variables est une application de
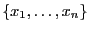 dans
dans
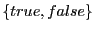 .
.
- Si
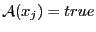 , alors
, alors 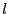 est
satisfait si
est
satisfait si 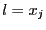 , non satisfait sinon
, non satisfait sinon
- si
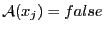 , alors
, alors 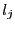 est
satisfait si
est
satisfait si 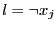 , non satisfait si
, non satisfait si 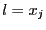
Une clause est satisfaite si au moins un des littéraux qui la forment
est satisfait. Une expression sous forme clausale est satisfaite si
toutes les clauses sont satisfaites. Le problème est le suivant :
- données :
 variables,
variables,  clauses de chacune
clauses de chacune 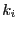 littéraux, chacun correspondant à une variable ou à la négation
d'une variable.
littéraux, chacun correspondant à une variable ou à la négation
d'une variable.
- question : trouver une affectation qui satisfasse toutes
les clauses (donc au moins un littéral par clause)
Ce problème (de satisfaction de contraintes) est NP-Complet dans le
cas général, et facile si les
clauses contiennent au plus 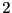 littéraux.. Remarquons que si la
question avait été "existe-t-il une affectation qui satisfasse toutes
les clauses ?'', ce problème serait un problème de décision.
littéraux.. Remarquons que si la
question avait été "existe-t-il une affectation qui satisfasse toutes
les clauses ?'', ce problème serait un problème de décision.




suivant: Couverture
monter: Problèmethèque
précédent: Voyageur de commerce
Table des matières
klaus
2010-08-05
![]() variables sous forme clausale
(conjonction de disjonctions), par exemple,
variables sous forme clausale
(conjonction de disjonctions), par exemple,